• Ibackshift Clutch Kit
• Backshift Meaning
• Backshift Hours Uk
• Backshift Rule

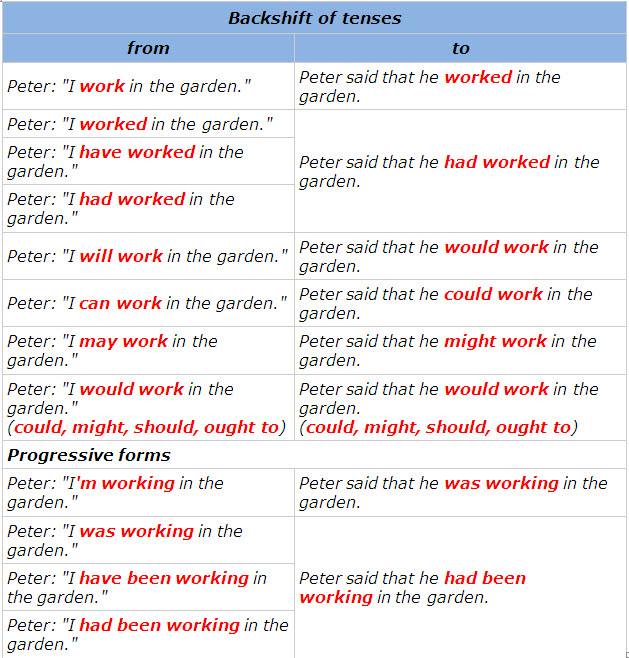
The Backshift Speed Boot is FXR’s Warmest Boot. With its 1200g of insulation it is rated to -75° C. It is extremely comfortable for endless miles of trail riding. It features a single anti-slip lace with molded lace sliders for easy tie & go use. uncountable (linguistics) the changing of a tense when reporting what somebody said, for example when reporting the words ‘What are you doing?’ as ‘He asked me what I was doing.’ See backshift in the Oxford Advanced American Dictionary.

In time series analysis, the lag operator (L) or backshift operator (B) operates on an element of a time series to produce the previous element. For example, given some time series

${\displaystyle X=\{X_1,X_2,\dots \}}$

then

${\displaystyle L{X}_t=X_{t-1}}$ for all ${\displaystyle t>1}$

or similarly in terms of the backshift operator B: ${\displaystyle B{X}_t=X_{t-1}}$ for all ${\displaystyle t>1}$. Equivalently, this definition can be represented as

${\displaystyle X_t=L{X}_{t+1}}$ for all ${\displaystyle t\ge 1}$

The lag operator (as well as backshift operator) can be raised to arbitrary integer powers so that

${\displaystyle L^{-1}{X}_t=X_{t+1}}$

and

${\displaystyle L^k{X}_t=X_{t-k}.}$

Lag polynomials[edit]

Polynomials of the lag operator can be used, and this is a common notation for ARMA (autoregressive moving average) models. For example,

${\displaystyle {\epsilon }_t=X_t-\sum _{i=1}^p{\phi }_i{X}_{t-i}=\left(1-\sum _{i=1}^p{\phi }_i{L}^i\right)X_t}$

specifies an AR(p) model.

A polynomial of lag operators is called a lag polynomial so that, for example, the ARMA model can be concisely specified as

${\displaystyle \phi (L)X_t=\theta (L){\epsilon }_t}$

where ${\displaystyle \phi (L)}$ and ${\displaystyle \theta (L)}$ respectively represent the lag polynomials

${\displaystyle \phi (L)=1-\sum _{i=1}^p{\phi }_i{L}^i}$

and

${\displaystyle \theta (L)=1+\sum _{i=1}^q{\theta }_i{L}^i.}$

Polynomials of lag operators follow similar rules of multiplication and division as do numbers and polynomials of variables. For example,

${\displaystyle X_t=\frac{\theta (L)}{\phi (L)}{\epsilon }_t,}$

means the same thing as

${\displaystyle \phi (L)X_t=\theta (L){\epsilon }_t.}$

As with polynomials of variables, a polynomial in the lag operator can be divided by another one using polynomial long division. In general dividing one such polynomial by another, when each has a finite order (highest exponent), results in an infinite-order polynomial.

An annihilator operator, denoted ${\displaystyle [{]}_{+}}$, removes the entries of the polynomial with negative power (future values).

Note that ${\displaystyle \phi \left(1\right)}$ denotes the sum of coefficients:

Ibackshift Clutch Kit

${\displaystyle \phi \left(1\right)=1-\sum _{i=1}^p{\phi }_i}$

Difference operator[edit]

Backshift Meaning

In time series analysis, the first difference operator :${\displaystyle \mathrm{\nabla }}$

Similarly, the second difference operator works as follows:

The above approach generalises to the i-th difference operator${\displaystyle {\mathrm{\nabla }}^i{X}_t=(1-L{)}^i{X}_t.}$

Conditional expectation[edit]

It is common in stochastic processes to care about the expected value of a variable given a previous information set. Let ${\displaystyle {\mathrm{\Omega }}_t}$ be all information that is common knowledge at time t (this is often subscripted below the expectation operator); then the expected value of the realisation of X, j time-steps in the future, can be written equivalently as:

${\displaystyle E[X_{t+j}|{\mathrm{\Omega }}_t]=E_t[X_{t+j}].}$

With these time-dependent conditional expectations, there is the need to distinguish between the backshift operator (B) that only adjusts the date of the forecasted variable and the Lag operator (L) that adjusts equally the date of the forecasted variable and the information set:

${\displaystyle L^n{E}_t[X_{t+j}]=E_{t-n}[X_{t+j-n}],}$

${\displaystyle B^n{E}_t[X_{t+j}]=E_t[X_{t+j-n}].}$

Backshift Hours Uk

See also[edit]

References[edit]

• Hamilton, James Douglas (1994). Time Series Analysis. Princeton University Press. ISBN0-691-04289-6.
• Verbeek, Marno (2008). A Guide to Modern Econometrics. John Wiley and Sons. ISBN0-470-51769-7.
• Weisstein, Eric. 'Wolfram MathWorld'. WolframMathworld: Difference Operator. Wolfram Research. Retrieved 10 November 2017.CS1 maint: discouraged parameter (link)
• Box, George E. P.; Jenkins, Gwilym M.; Reinsel, Gregory C.; Ljung, Greta M. (2016). Time Series Analysis: Forecasting and Control (5th ed.). New Jersey: Wiley. ISBN978-1-118-67502-1.

Backshift Rule